Expand all

Optimisation

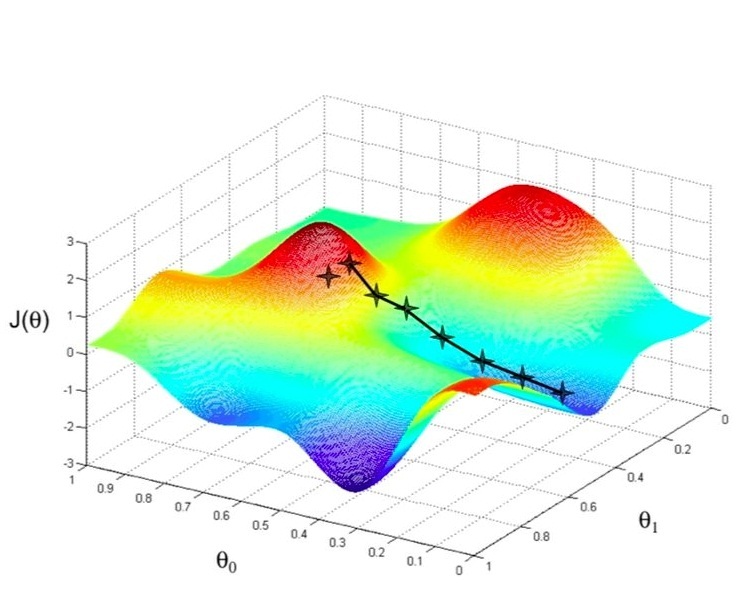
En conclusion, on peut noter que l’optimisation est une discipline mathématique  fondamentale. Il s’agit d’un processus de recherche de la meilleure solution à un problème donné, sous certaines contraintes. L’optimisation est un domaine d’application général et est appliqué dans un large éventail d’industries, y compris l’ingénierie, l’économie, la gestion et même la biologie. L’objectif est de trouver la valeur optimale pour une fonction donnée, connue sous le nom de fonction objectif, tout en satisfaisant toute une série de contraintes pouvant être des égalités ou des inégalités.

1. Modélisation du problème concret :

Dans un premier temps, on commence par analyser un problème réel et on le modélise mathématiquement. Cela implique de représenter la situation à l'aide d'une fonction mathématique qu'on cherche à maximiser ou minimiser. Les variables du problème sont identifiées et on établit les relations entre elles.

2. Formulation du problème d'optimisation :

Une fois le problème modélisé, il prend généralement la forme suivante :

  • Maximisation ou minimisation d'une fonction objectif
  • Sous des contraintes

3. Résolution du problème :

La résolution d'un problème d'optimisation peut se faire de manière analytique ou numérique :

  • Méthodes analytiques : Si la fonction et les contraintes sont suffisamment simples et continues, il est possible de trouver une solution exacte en utilisant des outils comme les dérivées (optimisation différentiable), les multiplicateurs de Lagrange (pour les contraintes d'égalités), ou d'autres théorèmes mathématiques comme le théorème de Karush-Kuhn-Tucker (KKT) dans le cas des contraintes inégales.
  • Méthodes numériques : Lorsque le problème est trop complexe ou que la solution exacte est difficile à obtenir, on utilise des méthodes d'optimisation numérique. Cela inclut des algorithmes comme :
    • La méthode du gradient (pour les problèmes différentiables),
    • La programmation linéaire (pour les problèmes linéaires),
    • Les algorithmes génétiques, la méthode de Newton, ou d'autres techniques adaptées aux problèmes non linéaires et aux grands systèmes.

Les programmes d'optimisation mathématique, qui résolvent ces problèmes numériquement, sont des outils puissants utilisés dans les applications industrielles, financières, scientifiques, et plus encore.


Mathematics2

The Mathematics course offers a comprehensive exploration of foundational mathematical concepts essential for understanding and analyzing complex systems in diverse scientific and engineering fields. This course encompasses the study of matrices, linear systems of equations, integration calculus, ordinary differential equations (ODEs), and multivariable functions, providing students with a robust toolkit for quantitative analysis and problem-solving.

Beginning with matrices and linear systems, students gain proficiency in matrix algebra, including operations, properties,  and determinants. Through theoretical study and practical applications, students learn to solve linear systems using techniques such as Gaussian elimination, matrix inversion, and matrix factorization, developing a deep understanding of the geometric and algebraic interpretations of solutions.

Integration calculus constitutes the next phase of the course, focusing on the Riemann Integral and its applications in computing areas, volumes, and accumulated quantities represented by continuous functions. Students explore techniques for calculating integrals, including integration by substitution, integration by parts, and partial fractions, gaining insights into the fundamental theorem of calculus and its implications for real-world modeling.

Moving beyond single-variable calculus, students delve into ordinary differential equations (ODEs), studying first-order and higher-order ODEs, as well as systems of ODEs. Through analytical study, students learn to solve ODEs and interpret their solutions in the context.

Finally, the course addresses multivariable functions, extending the concepts of differentiation and integration to functions of multiple variables. Students explore partial derivatives, gradients, etc...


Aérodynamique Théorique copie 1

Le cours consiste à énumérer les méthodes théoriques permettant le calcul des coefficients aérodynamiques pour le cas 2D (profil) et 3D (Aile et avion)

Chemistry practical 2023/2024

Chemistry practical is for 1 st  year students Institute of Aeronautics and Space Studies. 

Practical work can in fact facilitate learning . Using a practical activity can help structure a lesson and improve engagement and knowledge retention: Many students learn more easily by actually “doing”activities.

Different experiments are proposed to students. An experiment is a scientific test which is done in order to discover what happens to something in particular conditions.

métiers aéronautique

LES AERONEFS

Tous les appareils capables de s’élever ou décolle de sol et de circuler dans l'espace aérien sont des aéronefs. On distingue : les aérostats dont la sustentation est principalement assurée par la poussée d'Archimède, les aérodynes dont la sustentation résulte des forces aérodynamiques et enfin les aérospatiaux qui relèvent surtout de la balistique.

réglementation aéronautique

Preamble:

Welcome to the aeronautics course designed for second-year undergraduate and first-year master's students in the exciting field of aviation. This course aims to immerse you in the complex and captivating world of aviation, focusing on essential topics such as the establishment of the ICAO, international aeronautical institutions like EASA and FAA, as well as the organization of civil aviation in Algeria. We will also explore the various regulations and aeronautical standards, including Parts 21, 147, 66, and 145.

 

Summary:

This aeronautics course, designed for second-year undergraduate and first-year master's students, offers an in-depth exploration of the establishment of the ICAO (International Civil Aviation Organization) and its organization. We will begin by tracing the history of aviation and highlighting the circumstances that led to the creation of the ICAO in 1944 during the Chicago Convention. You will understand the significance of this historical event in harmonizing aviation standards and practices worldwide.

We will then review the articles of the Chicago Convention, the founding treaty of the ICAO, explaining each one in detail and showing how they have contributed to shaping the organization and its objectives. You will discover how the ICAO aims to promote the safety, regularity, and efficiency of air navigation across the globe.

A significant part of this course will be dedicated to the internal organization of the ICAO. You will learn more about the main bodies of the organization, such as the Assembly, the Council, and the Secretariat, as well as their roles and responsibilities. We will also examine how the ICAO collaborates with other international institutions and member states to achieve its goals.

Finally, we will analyze in detail the documents issued by the ICAO, including the annexes to the Convention, which detail standards and recommended practices in various areas of aviation. You will understand how these documents are used to regulate aviation operations at the international level.

This course offers you a comprehensive exploration of the establishment of the ICAO, its internal organization, and its role in regulating international aviation. You will gain a deep understanding of the history of aviation and the impact of the ICAO on the safety and efficiency of flights worldwide. Get ready for a fascinating dive into the world of international civil aviation!


Technical English 2

Technical English is designed to help students of Institute for Aeronautics and Aerospace Studies to improve their skills in this special field of Aeronautical Engineering. This lecture deals with different subjects related to the Aeronautics and Aviation areas. The main objectives for this is to develop their intellectual, personal and professional abilities to understand the original textbooks in aeronautics. The course is running in the first and second semester of every year beginning in September provided for underground level students (L2). Overall, Technical English gives students the language, information, and skills needed for their university program of study. It presents them with English from a variety of technological fields and situations, and develops their communication skills. The main objectives of this course are:

  1.  To Provide Technical English instruction to enhance students’ reading and writing in order to provide practice & interest in the language of Aeronautics and Aerospace Fields.
  2. To prepare students to sit for assessments and evaluations such as tests and quizzes in order to test and revise proper acquisition of the English language.
  3. To allow students to gain key strategies and expressions for communicating with professionals and non-specialists.


technique d'expression et de communication copie 2

ce cours est basée sur une méthodologie permettant aux nouveaux étudiants d’intégrer le monde de la communication orale et écrite . dans ce module, l'étudiant va apprendre à exprimer ses idées et surtout à s'exprimer oralement avec clarté et à développer ses compétences sur le plan personnel ou professionnel, dans le domaine de la communication et des techniques d’expression. au terme de ce cours , l'étudiant serait capable d'analyser et organiser une documentation , à en tirer l'essentiel et surtout pouvoir transmettre oralement ou par écrit l'idée retenue de cette documentation.

Travaux dirigés corrigés de traitement du signal

Le présent polycopié a été constitué par le recueil d’exercices, des épreuves de moyenne durée et de rattrapage données pendant les différents travaux dirigés à l’Institut d’aéronautique et des études spatiales de Blida. Ce recueil doit être considéré comme un prolongement des cours que reçoivent les étudiants.

Les exercices présentés dans ce fascicule restent, pour l’essentiel utile et constitue un outil de base destiné aux étudiants désirant s’initier au traitement du signal.

Les énoncés des exercices et corrigés de certains exercices associés sont donnés dans le même fascicule. Afin d’apprendre à résoudre les exercices proposés de manière personnelle et indépendante, le corrigé est donné à la fin de chaque série et ne devrait pas être consulté pendant les séances de travaux dirigés.